Circunferencia
La circunferencia es una curva plana y cerrada donde todos sus puntos están a igual distancia del centro.
|
La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro del círculo cuya superficie contiene.
Puede ser considerada como una elipse de excentricidad nula, o una elipse cuyos semiejes son iguales, o los focos coinciden. También se puede describir como la sección, perpendicular al eje, de una superficie cónica o cilíndrica, o como un polígono regular de infinitos lados, cuya apotema coincide con su radio
Elementos de la circunferencia[
Centro, es el punto interior equidistante de todos los puntos de la circunferencia;Existen varios puntos, rectas y segmentos, singulares en la circunferencia:
- Radio. El radio de una circunferencia es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma. El radio mide la mitad del diámetro.El radio es igual a la longitud de la circunferencia dividida entre 2π.
- Diámetro. El diámetro de una circunferencia es el segmento que une dos puntos de la circunferencia y pasa por el centro. El diámetro mide el doble del radio. El diámetro es igual a la longitud de la circunferencia dividida entre π;
- Cuerda. La cuerda es un segmento que une dos puntos de la circunferencia. El diámetro es la cuerda de longitud máxima.
- Recta secante. Es la línea que corta a la circunferencia en dos puntos;
- Recta tangente. Es la línea que toca a la circunferencia en un sólo punto;
- Punto de Tangencia es el punto de contacto de la recta tangente con la circunferencia;
- Arco. El arco de la circunferencia es cada una de las partes en que una cuerda divide a la circunferencia. Un arco de circunferencia se denota con el símbolo sobre las letras de los puntos extremos del arco.
- Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.
Formulas que se utilizan en una circunferencia
Ángulos en una circunferencia
Ángulo central, si tiene su vértice en el centro de esta. Sus lados contienen a dos radios.Un ángulo, respecto de una circunferencia, pueden ser:
La amplitud de un ángulo central es igual a la del arco que abarca.
Ángulo inscrito, si su vértice es un punto de la circunferencia y sus lados contienen dos cuerdas.
- La amplitud de un ángulo inscrito en una semi circunferencia equivale a la mayor parte del ángulo exterior que limita dicha base. (Véase: arco capaz.)
Ángulo semi-inscrito, si su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia.
- La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.
Ángulo interior, si su vértice está en el interior de la circunferencia.
- La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.
Ángulo exterior, si tiene su vértice en el exterior de la circunferencia
Longitud de la circunferencia[editar]
El interés por conocer la longitud de una circunferencia surge en Babilonia ( actual Irak), cuando usaban los carros con rueda, era primordial relacionar el diámetro o radio con la circunferencia.8
- La longitud
 de una circunferencia es:
de una circunferencia es:
donde  es la longitud del radio.
es la longitud del radio.
 es la longitud del radio.
es la longitud del radio.
Pues  (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
(número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
 (número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:
(número pi), por definición, es el cociente entre la longitud de la circunferencia y el diámetro:Área del círculo delimitado por una circunferencia
Ecuaciones de la circunferencia
Ecuación en coordenadas cartesianas
 .En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación
.En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación
Cuando el centro está en el origen (0, 0), la ecuación anterior se simplifica al
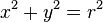 .
.
La circunferencia con centro en el origen y de radio la unidad, es llamada circunferencia goniométrica, circunferencia unidad o circunferencia unitaria.
De la ecuación general de una circunferencia,
se deduce:
resultando:
Si conocemos los puntos extremos de un diámetro:  ,
,
 ,
,
la ecuación de la circunferencia es:
Ecuación vectorial de la circunferencia[editar]
La circunferencia con centro en el origen y radio R, tiene por ecuación vectorial:  . Donde
. Donde  es el parámetro de la curva, además cabe destacar que
es el parámetro de la curva, además cabe destacar que 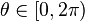 . Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
 . Donde
. Donde  es el parámetro de la curva, además cabe destacar que
es el parámetro de la curva, además cabe destacar que 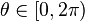 . Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
. Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
Sea C un punto fijo del plano, r un real positivo, P un punto cualquiera de ℝ2, la ecuación |P - C|= r es la ecuación vectorial de la circunferencia de centro C y radio r.9
Ecuación en coordenadas polares
Cuando el centro no está en el origen, sino en el punto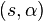 y el radio es
y el radio es  , la ecuación se transforma en:
, la ecuación se transforma en:
Ecuación paramétrica de la circunferencia
La circunferencia con centro en (a, b) y radio c se parametriza con funciones trigonométricas como:
y con funciones racionales como
 , donde t recorre todos los valores reales y se llama parámetro
, donde t recorre todos los valores reales y se llama parámetro



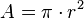 El
El 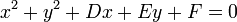





![x=a + c \cos t,\ y=b+c\,\sen\,t,\qquad t\in[0,2\pi]](http://upload.wikimedia.org/math/2/d/7/2d7135dd00d4c2a1ad1623a7a34212be.png)
No hay comentarios:
Publicar un comentario